Del 3 af 3: Sådan finder du værdi i populært spreadbet

Denne artikel er skrevet af Bjarke Eltard-Larsen, uddannet ingeniør, PhD og Seniorforsker på DTU. Artiklen, der er nummer tre ud af i alt tre i denne serie om spreadbetting, er bragt i et kommercielt samarbejde med SpreadEx*, som ikke har redaktionel indflydelse på indholdet. Du kan læse Del 1 via dette link og del 2 via dette link.

I de to første artikler har jeg skrevet om, hvad et spread er, og hvordan man kan regne prisen på et spread, samt hvilke overvejelser man skal gøre sig, når man staker.

Læs mere: Opret ny konto ved SpreadEx – og få stor kontantbonus og gratis Plusmedlemskab

I denne artikel vil jeg fokusere på en række nye markeder og vil samtidig diskutere, hvordan man ”reverse engineerer” bookmakernes model og kan benytte dette til at se, om ens ”hook” er medregnet i spreadet.

Nem måde at udregne målminutspreadet i spreadbetting

Mit første fokusområde er spreadet for målminutter. I denne form for væddemål bliver minuttallene for de enkelte mål lagt sammen, og det bliver sammenholdt det spread, man spillede til. Mål scoret i 45+ i første halvleg og 90+ i anden halvleg tæller som henholdsvis 45 og 90 i forhold til væddemålet. Dette marked har vores eksperter på Monetos spillet på mange gange både i de ugentlige podcasts og ’dagens spreadbet’ på hjemmesiden. Som så mange gange før har jeg hørt rigtig gode argumenter for, at mål kommer sent eller tidligt, men igen savner jeg argumenter for, hvorfor det gør, at der er værdi i spreadet (der er f.eks stor forskel på at spille til 150 eller 160 målminutter).

Hvordan bestemmes spreadet for målminutter? Den simpleste måde er at kigge på SpreadEx’s linjer og så at sige reverse engineere målminutspreadet. Målminutspreadet må afhænge meget af målspreadet på kampen, og derfor har jeg plottet målminutspreadet som funktion af målspreadet nedenfor (jeg har taget middelværdien mellem køb og salg) på en række kampe.

Her kan det tydeligt ses, at der er en ret lineær sammenhæng mellem målspreadet og spreadet for målminutter. Det ser derfor ud til, at man kan finde SpreadEx’s målminutterspread ved at gange målspreadet med 50.8. Det er stort set den samme faktor, man skal gange med for alle kampe jeg har kigget på, og det betyder at SpreadEx bruger den samme model uanset kampen og uanset ligaen. Dette er godt for bettere, som måske ikke kan finde værdi på målspreadlinjen, men har en ide om, at kampen alligevel vil starte langsomt. Hvis dette er tilfældet, vil overen potentielt være et godt spil, da man tror der vil komme få mål i starten men mange senere hen. Hvis man ikke kan finde værdi i målspreadet, er det afgørende, at man ser kampforløbet anderledes end andre kampe med et lignende målspread.

Læs mere: Ny i spreadbetting? Læs vores guide og kom nemt i gang

At SpreadEx benytter sig af den samme type model uanset kampen betyder også, at det er mindre vigtigt, at eksperterne forholder sig til prisen, så længe de argumenter, de nævner, ikke er fanget af de typiske algoritmer. Mine analyser tyder på, at de fleste algoritmer på sidemarkeder er ret simple, og derfor vil nogle argumenter ikke være med i prisen.

Hvis man alternativt godt kan finde værdi på over/under -markedet, men ikke synes at kampen udfolder sig markant anderledes end andre kampe med samme over/under-linje, kan man bruge nedenstående tabel til at finde prisen på målminutter. Her har jeg omdannet odds på over 2.5 mål (fair odds) til et målspread. Dette er gjort med poissonmodellen, som jeg viste stemte ret godt overens med SpreadEx’ model i den første artikel. Herefter har jeg ganget med de 50.8 for at få målminutspreadet.

Hvad siger data?

Indtil nu har jeg kun kigget på ovenstående spread ved at benytte mig af, hvad jeg tror SpreadEx’ faktor, som kan ganges på målspreadet, er, men hvad siger data egentlig?

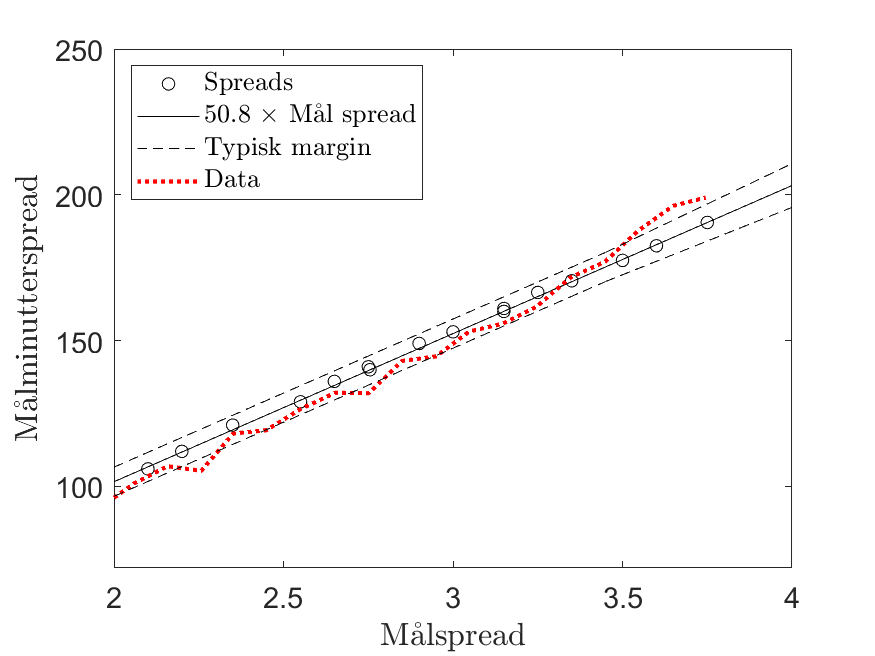
Nedenfor har jeg plottet den samme figur som før, men nu har jeg også tilføjet den typiske margin på SpreadEx’s målminutter spil og data fra de fem store ligaer for de sidste 10 år. For at beregne målspreadet for den faktiske data har jeg taget lukkeoddset hos Pinnacle på over 2.5 mål, fjernet margin og lavet det om til et målspread ved hjælp af poissonfordelingen. Værdierne på y-aksen er så fundet ved at regne det gennemsnitlige antal målminutter for alle kampe med pågældende målspread.

Figuren viser nogle ret interessante trends. For målspreads lavere end ca 3.3 er de faktisk oplevede målminutter lidt lavere end middelspreadet fra SpreadEx, men dog ikke generelt lavere end den margin, som SpreadEx typisk bruger på målminutterspreadet.

Hvordan kan det være, at data generelt ligger under? En forklaring kan være, at faktoren (50.8) engang har været anderledes, end den er i dag. I den nuværende sæson er der jo kommet ekstra tillægstid, og den ekstra tillægstid skal øge faktoren i forhold til sidste sæson. Det er ikke, fordi der kommer flere mål, for det er allerede inkorporeret i målspreadet, men fordi den ekstra tillægstid vil give en større andel af mål scoret i minut 45 og specielt minut 90. Data for de foregående 10 sæsoner har fulgt den røde linje, men for denne sæson kan vi forvente, at data vil ligge lidt højere end den røde linje og dermed tættere på middelspreadet. Min vurdering ud fra den ekstra tillægstid, der har været i denne sæson, er, at den røde linje vil flytte sig ca. 1-1.5 minut op og dermed ligge ret tæt (men lidt under) SpreadEx middelspread for de lave målspreads.

Der er også en anden interessant trend. Fra omkring målspread 3.3 ændres hældning på kurven, og ved de højere målspreads ligger de faktiske målminutter højere end SpreadEx’s typiske linje. Hvordan kan det være, at data generelt ligger under ved de lave målspreads og over ved de høje målspreads? Min bedste forklaring er, at hver gang der bliver scoret (som jo er mest sandsynligt ved de høje målspreads), så bliver der lagt mere tid til kampen. Dermed stiger sandsynligheden for et sent mål, og målminutspreadet må stige. Den simple lineære tilgang, som det ser ud til at SpreadEx benytter sig af, er med andre ord ikke helt dækkende for sådanne korrelationer.

Hvad betyder det for ens betting?

Generelt har jeg jo ikke fundet signifikant værdi på noget ved ovenstående øvelse. Det ville også være overraskende, da det har taget under en time at generere ovenstående. Jeg er dog ret interesseret i trenden ved de høje målspreads. Her ligger data lidt over den typiske margin fra SpreadEx. Da tillægstiden i denne sæson generelt er højere end tidligere, betyder det, at den røde linje skal rykkes op for denne sæson (da denne jo er bygget på data, hvor der blev spillet lidt kortere tid). Det kunne derfor tyde på, at for målspreads over ca. 3.5, vil der måske være (lille) værdi i blindt at spille over målminutterspreadet, og skal man lede efter værdi på målminutter ved høje mållinjer, så skal nok være overen, man skal kigge efter. Skal man spille under på målminutter giver det nok også mening at kigge mest på de lave målspreadlinjer.

SpreadEx ser ud til at benytte sig af en meget simpel model for målminutter. Dette betyder også, at nogle af de overvejelser omkring kampforløb, som vores eksperter benytter sig af typisk, ikke vil være inkluderet i målminutspreadet. Et eksempel kan være 1-1 testen. Hvis begge hold kan leve med 1-1, vil der typisk ikke komme så mange mål i slutningen af en kamp, og derfor kan der med stor sandsynlighed være værdi i at spille under på målminutter. Det er vigtigt at skrive, at jeg anser målspreadet som mere effektivt end målminutspreadet, og derfor kan 1-1 testen sagtens være inkluderet i målspreadet. Det er altså kun de afledte markeder, som målminutspreadet der ikke tager højde for det.

Avanceret reverse engineering

Nu viste jeg, hvordan man kan reverse engineer SpreadEx model ved målminutterspreadet. Faktisk tror jeg dog, at SpreadEx benytter sig af en noget mere avanceret model, som ikke kun udregner målminutter, men også kan give spreads på tidspunkt for første kampmål, andet kampmål, sidste kampmål osv. Har man sådan en model, kan man også nemt udregne målminutspreadet. Jeg tror derfor, at SpreadEx benytter sig af en model, hvor man antager en målrate for hvert minut i kampen og at summen af alle målraterne giver det samlede målspread. Med sådan en model kan man nemt finde alle spreads på måltider og målminutter.

Den simpleste form for model er at antage, at der er lige stor sandsynlighed for et mål i løbet af en kamp (dette et naturligvis ikke rigtigt). Laver man denne antagelse, vil man have følgende minutspread på 1-4 kampmål som funktion af målspreadet (her er det antaget, at der kommer tre min tillægstid i 1. halvleg og fem mintter i 2 halvleg):

Man kan se, at den simple model, jeg lige har opstillet, opfanger trends i SpreadEx linjer ganske godt, men forudser tidligere mål, end SpreadEx gør. Hvis man nu i stedet antager, at chancen for mål stiger lineært fra starten af kampen hen imod slutningen af kampen, så kan man få noget, der passer ret godt på SpreadEx’s linjer (hvis man prøver selv med en lineær trend eller en anden form for trend, så er det vigtigt, at integralet af funktionen giver det samme som målspreadet).

Nedenfor har jeg indsat en figur, der viser, hvor stor en andel af mål, der er scoret i et givent minut (alle minutter scoret i 45+ og 90+ er lagt i henholdsvis minut 45 og minut 90). Den sorte linje viser den faktiske data fra de fem store linjer, og den røde linje viser det, som jeg tror SpreadEx benytter sig af (eller i hvert fald det som passer ret godt med de øvrige markeder, som jeg vil vise lige om lidt). Jeg ville nok have brugt en lidt mindre hældning på linjen end den vist nedenfor, hvis jeg skulle matche data. Det kan dog ses, at en lineær stigning i målraten, som kampen skrider frem, passer ret godt med data. Det kan ses, at den lineære model overvurderer andelen af mål scoret i minut 45 og 90, men det er, fordi jeg har inkorporeret den ekstra spilletid i denne sæson.

Hvis jeg benytter den røde linje som input til min model for tidspunkt for mål 1-4 får jeg følgende resultat (vist med hele linjer). Det kan ses, at min fejl fra før ved den simple model nu er rettet ind, og min lineære model passer ret godt med SpreadEx’s linjer på tidspunkter for mål. Den passer også meget godt med SpreadEx typiske målminut faktor (50.8), som jeg diskuterede tidligere.

Hvad betyder det for ens betting?

SpreadEx ser ud til at benytte sig af en model, der tager udgangspunkt i målspreadet og herefter bruger en simpel tidsmodel til at beregne de afledte linjer. Næsten alle spreads, jeg har kigget på hos SpreadEx, passer godt på de modeller, jeg har sat op her. Det betyder altså, at argumenter om kampforløb typisk ikke vil være medtaget i linjen (det kan selvfølgelig godt være med i målspreadet, som jeg tror er ret effektivt). Tror man f.eks., at målspreadet passer meget godt, men at man er ret sikker på, at holdene vil komme mere aggressivt ud end andre kampe med samme målspread, ja så kan der nok godt være værdi i at spille under på tidspunkt for første mål, da dette argument nok ikke vil være medregnet i prisen. Det afgørende for, om denne type argumenter holder, er, at man sammenholder det med andre ”typiske” kampe med lignende målspread. Ved høje målspread vil de fleste hold jo komme ret aggressivt ud, så i disse tilfælde skal man altså have en ide om, at de vil komme ekstra aggressivt ud.

Steffen Dams yndlingsspread

Til sidst vil jeg tage en ny type spread op. Rainbow goals. Det er en af Steffen Dams nye yndlingsspreads, har han fortalt i de ugentlige podcasts, som du finder ved at klikke dig videre på denne side. På dette marked gives point alt efter, hvor mange mål der bliver scoret. Falder der 0 eller 5 eller flere mål, afgøres spillet med 25 point. Falder der 1 eller 4 mål, er det 10 point, og falder der 2 eller 3 mål, så er det 0 point.

Jeg vil i det følgende ikke diskutere, hvordan man kan finde værdi på dette marked, men i stedet vil jeg give en simpel formel for, hvordan man kan regne prisen på spreadet ud, hvis man er i stand til at sætte en række over/under linjer.

Husk at et spread findes ved at gange sandsynligheder for et udfald med de point det udfald giver. For rainbow goals er det altså:

Rainbow goals = p(0 mål)x25+p(1 mål)*10+p(2 mål)*0+p(3 mål)*0+p(4 mål)*10 +p(over 4 mål)*25

Jeg har kigget lidt på SpreadEx’ linjer for Rainbow goals og kan se, at de passer ret godt med en antaget poissonfordeling (som jeg også skrev om i artikel 1).

Nu er de fleste nok ikke vant til at regne den specifikke sandsynlighed for et bestemt antal mål ud, men i stedet sætte linjer på over/under x antal mål. Kan man gøre dettem, kan man også regne spreadet for rainbow goals ud, men formlen skal ændres lidt. Ud fra fair odds på over- og underlinjer skal rainbow-spreadet være:

Rainbow goals = 1/U05x25+(1/U15-1/U05)*10+1/O45*25+(1/O35-1/O45)*10

hvor U05 er fair odds på under 0.5 mål, U15 fair odds på under 1.5 mål, fair odds på over 3.5 mål og O45 fair odds på over 4.5 mål.

Steffen Dam har tit argumenteret for at spille under på rainbow goals, da han anser to og tre mål som meget sandsynlige, og 0 eller over 4,5 mål som meget usandsynlige. Jeg har som regel godt kunne følge hans argumenter, men har dog ikke været overbevist om, at de argumenter altid er nok til at slå SpreadEx’s margin. Hvis man har sådanne argumenter, og føler man kan sætte over/under linjerne nogenlunde præcist, kan man regne spreadet med ovenstående formel. Generelt vil jeg skrive, at skal man kunne finde værdi på rainbow goals, så skal man have solid værdi på enten over 0,5 mål eller under 4,5 mål (eller helst begge steder).

Jeg håber, at denne artikel og de to foregående inspirerer dig. Tak for at have læst helt hertil!